c4e_bigint.h File Reference
(Version 554)
Multi precision arithmetic in 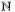 .
More...
.
More...
#include "c4e_elements.h"
Go to the source code of this file.
Functions | |
| C4eElemCmp | c4e_bigint_cmp (C4E_CONST C4eElement *a, C4E_CONST C4eElement *b) |
| Compares two (may be denormalized) big numbers. | |
| void | c4e_bigint_add (C4E_CONST C4eElement *a, C4E_CONST C4eElement *b, C4eElement *c) |
Addition of two big numbers 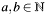 . . | |
| C4eSysBool | c4e_bigint_sub (C4E_CONST C4eElement *a, C4E_CONST C4eElement *b, C4eElement *c) |
The function subtracts two big numbers 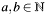 . . | |
| C4eSysBool | c4e_bigint_dec (C4E_CONST C4eElement *b, C4eElement *c) |
Decrements a big number 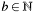 by 1. by 1. | |
| void | c4e_bigint_mul (C4E_CONST C4eElement *C4E_RESTRICT a, C4E_CONST C4eElement *C4E_RESTRICT b, C4eElement *C4E_RESTRICT c) |
Multiplication of two big numbers 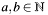 using the classical school book method. using the classical school book method. | |
| void | c4e_bigint_sqr (C4E_CONST C4eElement *C4E_RESTRICT b, C4eElement *C4E_RESTRICT c) |
Square of a big number 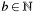 . . | |
| void | c4e_bigint_div (C4eElement *C4E_RESTRICT a, C4eElement *C4E_RESTRICT b, C4eElement *C4E_RESTRICT q) |
Division of two big numbers 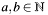 using the Pope and Stein algorithm. using the Pope and Stein algorithm. | |
| void | c4e_bigint_mod (C4eElement *C4E_RESTRICT a, C4eElement *C4E_RESTRICT b) |
Modulo division of two big numbers 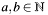 using the Pope and Stein algorithm. using the Pope and Stein algorithm. | |
| void | c4e_bigint_gcd (C4eElemTriple *a, C4eElemTriple *b, C4eArchSize n) |
Greatest Common Divisor of two numbers 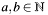 . It calculates the GCD of . It calculates the GCD of a->x and b->x together with the Bezout cofactors 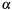 and and 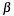 in equation in equation 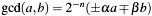 . . | |
Detailed Description
Multi precision arithmetic in 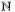 .
.
- Version:
- Id
- c4e_bigint.h 554 2015-03-09 16:50:11Z ralf
Definition in file c4e_bigint.h.
Function Documentation
| C4eElemCmp c4e_bigint_cmp | ( | C4E_CONST C4eElement * | a, | |
| C4E_CONST C4eElement * | b | |||
| ) |
Compares two (may be denormalized) big numbers.
- Parameters:
-
[in] a First number. [in] b Second number.
- Returns:
- The function returns:
- Return values:
-
C4eElemCmpGT if ais greater thanb;C4eElemCmpLT if ais less thanb;C4eElemCmpEQ if ais equal tob.
| void c4e_bigint_add | ( | C4E_CONST C4eElement * | a, | |
| C4E_CONST C4eElement * | b, | |||
| C4eElement * | c | |||
| ) |
Addition of two big numbers 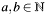 .
.
- Note:
- The parameters
aandbhave not to be normalized. But if they are normalized the resultcis normalized too.
- Precondition:
c->digitsmust point to pre-allocated memory space for at leastmax(a->size,b->size) + 1 digits.
- Parameters:
-
[in] a First summand. [in] b Second summand. [out] c Result of 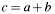 . It is allowed to set this argument pointing to
. It is allowed to set this argument pointing to aorbresp.c->digitspointing toa->digitsorb->digits(accumulator mode).
| C4eSysBool c4e_bigint_sub | ( | C4E_CONST C4eElement * | a, | |
| C4E_CONST C4eElement * | b, | |||
| C4eElement * | c | |||
| ) |
The function subtracts two big numbers 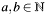 .
.
- Precondition:
c->digitsmust point to pre-allocated memory space for at leastmax(a->size,b->size) digits.
- Postcondition:
- The result
cis normalized in case it's sign (the return value) is positive, else it is not normalized.
- Parameters:
-
[in] a Minuend. [in] b Subtrahend. [out] c Result of 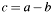 , if negative in two's-complement representation. It is allowed to set this parameter pointing to
, if negative in two's-complement representation. It is allowed to set this parameter pointing to aorbresp.c->digitspointing toa->digitsorb->digits(accumulator mode).
- Returns:
- Sign of result
- Return values:
-
C4E_FALSE if the result is positive C4E_TRUE if the result is negative. In that case cis in two's-complement representation of sizeb->size.
- See also:
- C4eElement, C4E_ELEM_ASGN_MEM()
| C4eSysBool c4e_bigint_dec | ( | C4E_CONST C4eElement * | b, | |
| C4eElement * | c | |||
| ) |
Decrements a big number 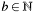 by 1.
by 1.
- Note:
- If a negative result is indicated, the caller might add 1 to recover the original value.
- Precondition:
c->digitsmust point to pre-allocated memory space for at leastb->sizedigits.
- Parameters:
-
[in] b The number to decrement. [out] c Result 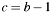 , which may alias
, which may alias b.
- Returns:
- Sign of result
- Return values:
-
C4E_FALSE if the result is positive C4E_TRUE if the result is negative. In that case cis in two's-complement representation, with the same size asb.
- See also:
- C4eElement, C4E_ELEM_ASGN_MEM()
| void c4e_bigint_mul | ( | C4E_CONST C4eElement *C4E_RESTRICT | a, | |
| C4E_CONST C4eElement *C4E_RESTRICT | b, | |||
| C4eElement *C4E_RESTRICT | c | |||
| ) |
Multiplication of two big numbers 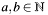 using the classical school book method.
using the classical school book method.
- Note:
- If
aandbare normalized thencis normalized too. In the other casescis not normalized. Ifcis normalized, then the resulting size isa->size+b->sizeora->size+b->size- 1. -
Because this function implements the classical school book algorithm, it's complexity is O(
a->size*b->size).
- Precondition:
- Use of restrict qualifier indicates that aliasing
aorbwithcor aliasinga->digitsorb->digitswithc->digitsis not allowed. -
c->digitsmust point to pre-allocated memory space for at least (a->size+b->size) digits.
- Parameters:
-
[in] a First multiplier. [in] b Second multiplier. [out] c Result 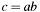 .
.
- See also:
- C4eElement, C4E_ELEM_ASGN_MEM()
| void c4e_bigint_sqr | ( | C4E_CONST C4eElement *C4E_RESTRICT | b, | |
| C4eElement *C4E_RESTRICT | c | |||
| ) |
Square of a big number 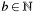 .
.
- Note:
- This algorithm has complexity
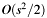 for large
for large 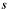 (equivalent
(equivalent b->size). -
The algorithm is derived directly from the school book multiplication method. With
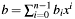 , where
, where 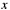 is the radix, it is based on the following simplification:
is the radix, it is based on the following simplification: 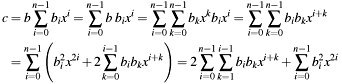
- Precondition:
- Use of restrict qualifier indicates that aliasing
bwithcor aliasingb->digitswithc->digitsis not allowed. -
c->digitsmust point to pre-allocated memory space for at least (2 *b->size) digits, at minimum one digit.
- Parameters:
-
[in] b Argument to be squared. [out] c Result 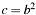 .
.
- See also:
- C4eElement, C4E_ELEM_ASGN_MEM()
| void c4e_bigint_div | ( | C4eElement *C4E_RESTRICT | a, | |
| C4eElement *C4E_RESTRICT | b, | |||
| C4eElement *C4E_RESTRICT | q | |||
| ) |
Division of two big numbers 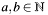 using the Pope and Stein algorithm.
using the Pope and Stein algorithm.
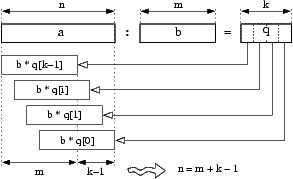
Multi-Precision Division
- Note:
- The asymptotic complexity of the algorithm is O(
a->size*b->size).
- Attention:
- Divisor
bis temporary modified - so it must be writable. After function return it holds the same value as at function entry.
- Precondition:
- The numbers
aandbmust be normalized. -
Divide by zero is not supported - catch this situation in advance (using macro C4E_ELEM_IS_ZERO(
b)). -
Use of restrict qualifier indicates that aliasing
awithbor aliasinga->digitswithb->digitsis not allowed. -
Because
a->digitsis also used as workplace, there must be pre-allocated memory space for at least (a->size+ 1) digits. -
q->digitsmust point to pre-allocated memory space for at least (a->size-b->size+ 1) digits.
- Bibliography:
D. A. Pope and M. L. Stein: Multiple Precision Arithmetic. CACM, 3:652-654, 1960
G. E. Collins and D. R. Musser: Analysis of the Pope- Stein Division Algorithm. University of Wisconsin Computer Sciences Department, Technical Report #55, Jan 1969
D. E. Knuth: The Art of Computer Programming, Vol. 2 (Semi-Numerical Algorithms). Addison-Wesley, 1997
- Parameters:
-
[in,out] a Dividend as input, remainder 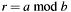 as output.
as output. [in] b Divisor (temporary modified). [out] q Integer quotient q = floor(a / b). If qis NULL then no quotient will be returned.
- See also:
- C4eElement, C4E_ELEM_ASGN_MEM()
| void c4e_bigint_mod | ( | C4eElement *C4E_RESTRICT | a, | |
| C4eElement *C4E_RESTRICT | b | |||
| ) |
Modulo division of two big numbers 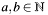 using the Pope and Stein algorithm.
using the Pope and Stein algorithm.

Multi-Precision Division
- Note:
- The asymptotic complexity of the algorithm is O(
a->size*b->size).
- Attention:
- Divisor
bis temporary modified - so it must be writable. After function return it holds the same value as at function entry.
- Precondition:
- The numbers
aandbmust be normalized. -
Divide by zero is not supported - catch this situation in advance (using macro C4E_ELEM_IS_ZERO(
b)). -
Use of restrict qualifier indicates that aliasing
awithbor aliasinga->digitswithb->digitsis not allowed. -
Because
a->digitsis also used as workplace, there must be pre-allocated memory space for at least (a->size+ 1) digits.
- Bibliography:
D. A. Pope and M. L. Stein: Multiple Precision Arithmetic. CACM, 3:652-654, 1960
G. E. Collins and D. R. Musser: Analysis of the Pope- Stein Division Algorithm. University of Wisconsin Computer Sciences Department, Technical Report #55, Jan 1969
D. E. Knuth: The Art of Computer Programming, Vol. 2 (Semi-Numerical Algorithms). Addison-Wesley, 1997
- Parameters:
-
[in,out] a Dividend as input, remainder 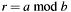 as output.
as output. [in] b Divisor (temporary modified).
- See also:
- C4eElement, C4E_ELEM_ASGN_MEM()
| void c4e_bigint_gcd | ( | C4eElemTriple * | a, | |
| C4eElemTriple * | b, | |||
| C4eArchSize | n | |||
| ) |
Greatest Common Divisor of two numbers 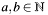 . It calculates the GCD of
. It calculates the GCD of a->x and b->x together with the Bezout cofactors 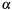 and
and 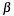 in equation
in equation 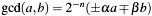 .
.
- Note:
- If
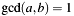 the algorithm computes
the algorithm computes 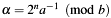 in
in a->yand returnsa->xina->z,b->xinb->z, ifnis zero. -
If
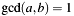 and for example also
and for example also 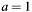 applies, then the Bezout cofactors will become (for this case):
applies, then the Bezout cofactors will become (for this case): 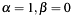 , independent of the value of
, independent of the value of 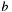 .
. -
The asymptotic complexity of the algorithm is O(
a->x.size*b->x.size). -
The coprime part
a->zresp.b->zmeans: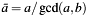 resp.
resp. 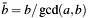 . With respect to Bezout's identity it satisfies the following equation:
. With respect to Bezout's identity it satisfies the following equation:
means![\[\gcd(\bar{a},\bar{b}) = \alpha\bar{a} + \beta\bar{b} = 1 \]](form_32.png)
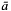 and
and 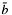 are really coprime. Modular division of the identity above gives:
are really coprime. Modular division of the identity above gives: 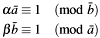
- Precondition:
- The numbers
a->xandb->xmust be normalized, e.g. using function c4e_elem_norm(). -
It is not allowed that both numbers
a->xandb->xare both zero (C4E_ELEM_IS_ZERO()). -
The required digits space (in units of C4eArchDigit) for all big numbers is the maximum size of the two input values
a->xandb->xplus (n/ C4E_SYS_DIGIT_BITS + 1) digits.
- Bibliography:
J. Stein: Computational problems associated with Racah algebra. Journal of Computational Physics, 1, 1967.
Bojanczyk, A. and R. P. Brent: A systolic algorithm for extended GCD computation. Computers & Mathematics with Applications, 14(4):233-238, 1987.
Burton S. Kaliski: The Montgomery Inverse and Its Applications. IEEE Transactions on Computers, 44(8):1064-1065, August 1995.
- Parameters:
-
[in,out] a As an input parameter a->xholds the number, for which the GCD withb->xis calculated. As an output it returns:- zero in
a->x; - Bezout cofactor
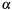 in
in a->y; - the coprime part of
a->xina->z; - sign of cofactor in
a->attr(0 if positive).
[in,out] b As an input parameter b->xholds the number, for which the GCD witha->xis calculated. As an output it returns:- the
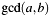 in
in b->x; - Bezout cofactor
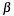 in
in b->y; - the coprime part of
b->xinb->z; - sign of cofactor in
b->attr(0 if positive).
[in] n The number nin equation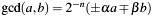 . If
. If nis zero it returns simply the Bezout cofactors in equation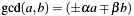 .
. - zero in
 1.6.1
1.6.1