c4e_ec.h File Reference

(Version 567)

Elliptic curve (EC) domain basics. More...

#include "c4e_elements.h"

Include dependency graph for c4e_ec.h:

Data Structures
struct	C4eEcDomain
	Elliptic Curve domain parameters. More...
Defines
#define	C4E_EC_PTFMT_PC_Y
#define	C4E_EC_PTFMT_PC_C
#define	C4E_EC_PTFMT_PC_U
#define	C4E_EC_PTFMT_PC_H
#define	C4E_EC_GF_BYTES_MAX
	Maximum size of a field element in the underlying prime field 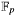$\mathbb{F}_p$ or binary field $\mathbb{F}_{2^n}$ , in bytes.
#define	C4E_EC_ATTR_NONE
#define	C4E_EC_ATTR_INF
#define	C4E_EC_ASGN_MEM(pt, mem, size)
	Assign digits memory to an EC point x- and y-coordinate.
#define	C4E_EC_IS_ZERO(pt)
	Checks whether an EC point is zero (at infinity) or not.
#define	C4E_EC_SET_INIT(pt)
	Sets an EC point (attribute) to it's initial (default) value.
#define	C4E_EC_SET_ZERO(pt)
	Sets an EC point (at infinity) to zero.
#define	C4E_EC_ASSERT_PTR(pt)
	Assert the pointer members in an EC point structure.
#define	C4E_EC_FIELD_BITS_MAX(mbits)
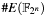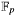	Maximum size calculation for elliptic curve order (also designated as $\#E(\mathbb{F}_{2^n})$ ) from the size of ground field $\mathbb{F}_{2^n}$ or $\mathbb{F}_p$ , in bits.
#define	C4E_EC_FIELD_BYTES_MAX(mlen)
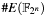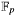	Maximum size calculation for elliptic curve order (also designated as $\#E(\mathbb{F}_{2^n})$ ) from the size of ground field $\mathbb{F}_{2^n}$ or $\mathbb{F}_p$ , in bytes.
#define	C4E_EC_FIELD_DIGITS_MAX(msize)
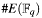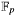	Maximum size calculation for elliptic curve order (also designated as $\#E(\mathbb{F}_{q})$ ) from the size of ground field $\mathbb{F}_{2^n}$ or $\mathbb{F}_p$ , in digits.
Typedefs
typedef C4eElemPair	C4eEcPoint
	Elliptic Curve (EC) point.

Detailed Description

Elliptic curve (EC) domain basics.

Author:: Copyright (C) 2014-2015 Ralf Hoppe <ralf.hoppe@ieee.org>

Version:

Id: c4e_ec.h 567 2015-05-17 13:27:06Z ralf

Definition in file c4e_ec.h.

Define Documentation

#define C4E_EC_ATTR_NONE

none (default) attribute for C4eEcPoint::attr.

Definition at line 198 of file c4e_ec.h.

#define C4E_EC_ATTR_INF

Indicates an EC point at infinity, in C4eEcPoint::attr.

Definition at line 203 of file c4e_ec.h.

#define C4E_EC_ASGN_MEM	(	pt,
		mem,
		size	)

Assign digits memory to an EC point x- and y-coordinate.

Parameters:

`[in]`	pt	Pointer to EC point which must have digits memory assigned to x- and y-coordinate.
`[in]`	mem	Digits memory (of type C4eArchDigit*) to be assigned to `pt->x` and `pt->y`.
`[in]`	size	Number of digits to be assigned to digits pointers of `pt->x` and `pt->y`.

See also:: C4eEcPoint

Definition at line 226 of file c4e_ec.h.

#define C4E_EC_IS_ZERO ( pt )

Checks whether an EC point is zero (at infinity) or not.

Parameters:

[in] pt Pointer to EC point.

Returns:: C4E_TRUE if point is zero, else C4E_FALSE.

Definition at line 244 of file c4e_ec.h.

#define C4E_EC_SET_INIT ( pt )

Sets an EC point (attribute) to it's initial (default) value.

Parameters:

[in] pt Pointer to EC point.

Definition at line 254 of file c4e_ec.h.

#define C4E_EC_SET_ZERO ( pt )

Sets an EC point (at infinity) to zero.

Parameters:

[in] pt Pointer to EC point.

See also:: C4E_EC_IS_ZERO()

Definition at line 265 of file c4e_ec.h.

#define C4E_EC_ASSERT_PTR ( pt )

Assert the pointer members in an EC point structure.

Note:: This macro may be usual for output parameters checking.

Parameters:

[in] pt Pointer to EC point of type C4eEcPoint.

Definition at line 276 of file c4e_ec.h.

#define C4E_EC_FIELD_BITS_MAX ( mbits )

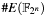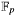Maximum size calculation for elliptic curve order (also designated as $\#E(\mathbb{F}_{2^n})$ ) from the size of ground field $\mathbb{F}_{2^n}$ or $\mathbb{F}_p$ , in bits.

From Hasse's theorem (see for example ANSI X9.63, annex B.3 and B.4) it is known that:

$q + 1 - 2 \sqrt{q} \le \#E(\mathbb{F}_q) \le q + 1 + 2 \sqrt{q}$

Because we have three summands at the right side, we may have two bits of overflow, when adding all together. So the number of bits for 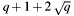$q + 1 + 2 \sqrt{q}$ is the number of bits used by q plus 2.

Note:: Because of 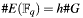$\#E(\mathbb{F}_q) = h \#G$ and so 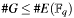$\#G \le \#E(\mathbb{F}_q)$ this is also the maximum order of base point G.

Bibliography:: Public Key Cryptography For The Financial Services Industry: Key Agreement and Key Transport Using Elliptic Curve Cryptography. ANSI X9.63, 2001.

Parameters:

[in] mbits Size of modulus (a prime number or binary polynomial) in bits, for example calculated by use of function c4e_elem_bits().

Returns:: Maximum number of bits the order of elliptic curve E may consist of.

Definition at line 316 of file c4e_ec.h.

#define C4E_EC_FIELD_DIGITS_MAX ( msize )

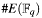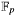Maximum size calculation for elliptic curve order (also designated as $\#E(\mathbb{F}_{q})$ ) from the size of ground field $\mathbb{F}_{2^n}$ or $\mathbb{F}_p$ , in digits.

Note:: In contrast the minimum size (in digits) of curve order C4eEcDomain::q is msize - 1U.

Definition at line 359 of file c4e_ec.h.

c4e_ec.h File Reference

(Version 567)

Data Structures

Defines

Typedefs

Detailed Description

Define Documentation