C4eEcDomain Struct Reference
[Elliptic Curve Cryptography (ECC)]
Elliptic Curve domain parameters. More...
#include <c4e_ec.h>
Data Fields | |
| C4eElemOsp | m |
| C4eElement | a |
| C4eElement | b |
| C4eElemOsp | q |
| C4eEcPoint | g |
| C4eElement | h |
Detailed Description
Elliptic Curve domain parameters.
- Note:
- All elements must be normalized, for example by by using functions c4e_elem_norm() or c4e_elem_os2e().
- Bibliography:
- Polk, W., Housley, R. and L. Bassham: Algorithms and Identifiers for the Internet X.509 Public Key Infrastructure Certificate and Certificate Revocation List (CRL) Profile. RFC 3279, IETF, April 2002.
- Bibliography:
- Standard Specifications For Public-Key Cryptography. Std 1363-2000, IEEE, 2000.
- See also:
- C4eEcPoint, C4eElement, C4E_ELEM_ASGN_MEM()
Definition at line 60 of file c4e_ec.h.
Field Documentation
Prime number p or irreducible polynomial m(x) and also the maximum size of a field element in the underlying prime field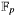 
or binary field 
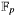, in bytes (for example 128U for a 1024 bit modulus in or 21U for NIST curve B-163 in ). If C4E_EC_GF_BYTES_MAX is defined, then m.len must be less/equal than C4E_EC_GF_BYTES_MAX.
- Note:
- In 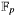all calculations are modulo the prime number p (C4eEcDomain::m). So the size of a field element is always less/equal than p. Therefore m.len also specifies the nominal size of p.
-
But in binary field the size of each field element is one bit less than the size of modulus (the irreducible polynomial m(x) in C4eEcDomain::m). For example the ANSI curve from [X9.62, J.4.2], having modulus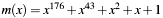
, needs 177 bit for representing the modulus, but the field elements do have a maximum size of 176 bit. So member m.len can be calculated by: for this curve.C4E_SYS_DIV_CEIL(176U, 8U)
- See also:
- C4E_EC_GF_BYTES_MAX
Order of base point C4eEcDomain::g, a prime number. The order of elliptic curve E can be calculated by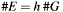 
. The length of G in q.len also determines the length of an ECDSA signature, which is: 2U * q.len.
- Note:
- For nearly all well-known elliptic curves q.len is less than or equal to m.len, especially when the Hasse interval is small (see C4E_EC_FIELD_BITS_MAX()). But for special (very uncommon/rare) curves q.len respective q.val.size might be greater than m.len respective m.val.size. Macros C4E_EC_FIELD_BYTES_MAX() and C4E_EC_FIELD_DIGITS_MAX() reflect this situation (for this kind of elliptic curves).
-
The number of digits needed by q.val can be calculated by: which is the preferred method, or by:
C4E_ELEM_DIGITS_NUM(dom->q.len)
C4E_EC_FIELD_DIGITS_MAX(dom->m.val.size)
- Attention:
- Member q.val sometimes is modified (temporary) when using functions, which deal with modular reduction, for example ECDSA. Therefore it must be writable and mutual exclusive accessible in most situations.
- See also:
- C4E_EC_FIELD_DIGITS_MAX()
Base point G of an elliptic curve, which has (prime) order C4eEcDomain::q.
Cofactor: order of the elliptic curve E (number of points on E) divided by the order of base point G (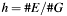
), which is a big number less than #E.
- Note:
- This element is only used by functions c4e_ecc2n_dh() and c4e_eccp_dh(), when performing ECDH with cofactor multiplication (ECDHC). If ECDHC should not be used (or ECDH at all is not used) then you are allowed to set it invalid, using macro C4E_ELEM_SET_ZERO(). There is no need to assign memory to h.digits in this case.
The documentation for this struct was generated from the following file:
