c4e_gf2n.h File Reference
(Version 551)
Polynomial arithmetic in finite field  .
More...
.
More...
#include "c4e_mod2n.h"
Include dependency graph for c4e_gf2n.h:
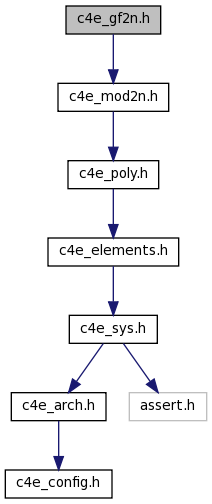
Go to the source code of this file.
Defines | |
| #define | C4E_GF2N_INV_SPACE(msize) |
| Temp. space calculation (in units of C4eArchDigit) for function c4e_gf2n_inv(). | |
Functions | |
| void | c4e_gf2n_inv (C4E_CONST C4eElement *C4E_RESTRICT a, C4E_CONST C4eElement *C4E_RESTRICT b, C4E_CONST C4eElement *C4E_RESTRICT m, C4eArchDigit tmp[], C4eElement *C4E_RESTRICT c) |
Inversion of a field element in  , with multiplication by another element (so performing a division). , with multiplication by another element (so performing a division). | |
| C4eSysStatus | c4e_gf2n_qsolve (C4E_CONST C4eElement *C4E_RESTRICT m, C4E_CONST C4eElement *C4E_RESTRICT beta, C4eArchDigit tmp[C4E_RESTRICT], C4eElement *C4E_RESTRICT z) |
Solves the quadratic equation 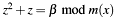 in in  . . | |
Detailed Description
Polynomial arithmetic in finite field  .
.
- Version:
- Id
- c4e_gf2n.h 551 2015-03-01 12:37:45Z ralf
Definition in file c4e_gf2n.h.
Define Documentation
| #define C4E_GF2N_INV_SPACE | ( | msize | ) |
Temp. space calculation (in units of C4eArchDigit) for function c4e_gf2n_inv().
- Parameters:
-
[in] msize Size of binary polynomial m(x) in C4eArchDigit units.
- Returns:
- Required digit space (in units of C4eArchDigit) when using c4e_gf2n_inv() or functions based on it.
- See also:
- c4e_gf2n_inv()
Definition at line 49 of file c4e_gf2n.h.
Function Documentation
| void c4e_gf2n_inv | ( | C4E_CONST C4eElement *C4E_RESTRICT | a, | |
| C4E_CONST C4eElement *C4E_RESTRICT | b, | |||
| C4E_CONST C4eElement *C4E_RESTRICT | m, | |||
| C4eArchDigit | tmp[], | |||
| C4eElement *C4E_RESTRICT | c | |||
| ) |
Inversion of a field element in  , with multiplication by another element (so performing a division).
, with multiplication by another element (so performing a division).
- Precondition:
- The polynomials
aandmmust be normalized (e.g. by using function c4e_elem_norm()) and must be unequal to zero. -
The polynomials
aandbmust be reduced tom(e.g. by using c4e_poly_mod(), so having a size which is less/equal than the size ofm). -
tmpmust point to pre-allocated memory space for at least (3U * C4E_GF2N_INV_SPACE(m->size)) digits. -
Use of restrict qualifier indicates that aliasing
aorbwithcor aliasinga->digitsorb->digitswithc->digitsis not allowed.
- Bibliography:
- Hankerson, Darrel, Alfred Menezes und Scott Vanstone: Guide to Elliptic Curve Cryptography. Springer, New York, 2004.
- Bibliography:
- Crandall, Richard und Carl Pomerance: Prime Numbers. A Computational Perspective. Springer, 2. Auflage, 2005.
- Parameters:
-
[in] a Binary polynomial to be inverted modulo the polynomial m.[in] b Binary polynomial to be multiplied with 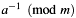 or NULL if only the element inversion is of interest (assumes
or NULL if only the element inversion is of interest (assumes b= 1).[in] m Binary polynomial forming the modulus of the associated field  .
. tmp Array of temporary space elements (see preconditions for details on size). [out] c Binary polynomial which is 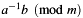 , normalized. If the result is zero then
, normalized. If the result is zero then aseems not to be a valid field element (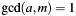 does not hold true) and so does not have an inverse (error condition). The required C4eArchDigit digits space is C4E_GF2N_INV_SPACE(
does not hold true) and so does not have an inverse (error condition). The required C4eArchDigit digits space is C4E_GF2N_INV_SPACE(m->size).
| C4eSysStatus c4e_gf2n_qsolve | ( | C4E_CONST C4eElement *C4E_RESTRICT | m, | |
| C4E_CONST C4eElement *C4E_RESTRICT | beta, | |||
| C4eArchDigit | tmp[C4E_RESTRICT], | |||
| C4eElement *C4E_RESTRICT | z | |||
| ) |
Solves the quadratic equation 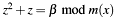 in
in  .
.
- Precondition:
tmpmust point to pre-allocated memory space for at least (4U *m->size) digits.-
The polynomial
mmust be normalized (e.g. by using function c4e_elem_norm()) and it must be unequal to zero. Ifmis not irreducible (which normally is a precondition for the existence of field then this function may return error C4E_STATUS_EDOM.
then this function may return error C4E_STATUS_EDOM. -
The size of polynomial
betamust be less/equalm->size(in best-case it is also reduced tom). -
Use of restrict qualifier indicates that aliasing any of the argument pointers with the result pointer
zis not allowed.
- Bibliography:
- Standard Specifications For Public-Key Cryptography. Std 1363-2000, IEEE, 2000.
- Bibliography:
- Public Key Cryptography For The Financial Services Industry: The Elliptic Curve Digital Signature Algorithm (ECDSA). ANSI X9.62, 1998.
- Parameters:
-
[in] m Binary polynomial forming the modulus of the associated field  .
. [in] beta Right hand side of quadratic equation (value zero is allowed, then zbecomes zero).tmp Temporary used memory space of (4U * m->size) digits.[out] z Result 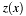 in equation
in equation 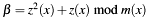 , not normalized. The other solution then is
, not normalized. The other solution then is 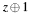 . The required C4eArchDigit digits space for
. The required C4eArchDigit digits space for zism->size.
- Returns:
- Validity status of result
z.
- Return values:
-
C4E_STATUS_OK if the result is valid C4E_STATUS_ERNG random generator failure C4E_STATUS_EDOM no solution in 
 1.6.1
1.6.1