c4e_poly.h File Reference

(Version 551)

Polynomial arithmetic with coefficients from $ \mathbb{F}_2 $. More...

#include "c4e_elements.h"
Include dependency graph for c4e_poly.h:

Go to the source code of this file.

Functions

C4eElemCmp c4e_poly_cmp (C4E_CONST C4eElement *a, C4E_CONST C4eElement *b)
 Compares two (may be denormalized) binary polynomials.
void c4e_poly_add (C4E_CONST C4eElement *a, C4E_CONST C4eElement *b, C4eElement *c)
 Addition of two binary polynomials (with coefficients in 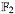$ \mathbb{F}_2$).
void c4e_poly_addshl (C4E_CONST C4eElement *a, C4E_CONST C4eElement *b, C4eArchSize shift, C4eElement *c)
 Addition of a binary polynomial with a (bit-wise) left-shifted binary polynomial.
void c4e_poly_mul (C4E_CONST C4eElement *C4E_RESTRICT a, C4E_CONST C4eElement *C4E_RESTRICT b, C4eElement *C4E_RESTRICT c)
 Multiplication of two binary polynomials (with coefficients in 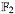$ \mathbb{F}_2$).
void c4e_poly_sqr (C4E_CONST C4eElement *a, C4eElement *c)
 Square of a binary polynomial (with coefficients in 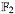$ \mathbb{F}_2$).
void c4e_poly_mod (C4E_CONST C4eElement *C4E_RESTRICT a, C4E_CONST C4eElement *C4E_RESTRICT b, C4E_CONST C4eElement *C4E_RESTRICT m, C4eElement *C4E_RESTRICT c)
 Modulo-division of two binary polynomials (reduction), with optional pre-multiplication by a third polynomial.
void c4e_poly_gcd (C4eElemTriple *a, C4eElemTriple *b)
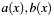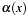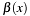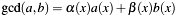 Greatest Common Divisor of two binary polynomials $ a(x),b(x) $ over $ \mathbb{F}_2 $. It calculates the GCD of a->x and b->x together with the Bezout cofactors $ \alpha(x) $ and $ \beta(x) $ in equation $ \gcd(a,b)=\alpha(x) a(x) + \beta(x) b(x) $.

Detailed Description

Polynomial arithmetic with coefficients from $ \mathbb{F}_2 $.

Note:
This interface is the counterpart to c4e_bigint.h.
Author:
Copyright (C) 2013-2015 Ralf Hoppe <ralf.hoppe@ieee.org>
Version:
Id
c4e_poly.h 551 2015-03-01 12:37:45Z ralf

Definition in file c4e_poly.h.

Function Documentation

C4eElemCmp c4e_poly_cmp ( C4E_CONST C4eElement *  a,
C4E_CONST C4eElement *  b 
)

Compares two (may be denormalized) binary polynomials.

Parameters:
[in] a First polynomial.
[in] b Second polynomial.
Returns:
The function returns:
Return values:
C4eElemCmp::C4eElemCmpGT in case the degree of a is greater than the degree b;
C4eElemCmp::C4eElemCmpLT in case the degree of a is less than the degree b (or both have the same degree but the content differs);
C4eElemCmp::C4eElemCmpEQ if both polynomials have the same degree and the same content.
void c4e_poly_add ( C4E_CONST C4eElement *  a,
C4E_CONST C4eElement *  b,
C4eElement *  c 
)

Addition of two binary polynomials (with coefficients in 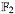$ \mathbb{F}_2$).

Note:
The parameters a and b have not to be normalized, except for performance reasons.
Parameters:
[in] a First polynomial.
[in] b Second polynomial.
[out] c Result 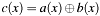$ c(x) = a(x) \oplus b(x) $, not normalized. It is allowed to set c pointing to a or b.
void c4e_poly_addshl ( C4E_CONST C4eElement *  a,
C4E_CONST C4eElement *  b,
C4eArchSize  shift,
C4eElement *  c 
)

Addition of a binary polynomial with a (bit-wise) left-shifted binary polynomial.

Note:
It is allowed to set c pointing to a or b.
Precondition:
The required digits space (in units of C4eArchDigit) for c is: max(b->size + ceil(shift / C4E_SYS_DIGIT_BITS), a->size)
Parameters:
[in] a Pointer to first binary polynomial.
[in] b Pointer to second binary polynomial.
[in] shift Number of bits to shift each digit in b before xor'ing with a.
[out] c Result c = a ^ (b << shift), normalized.
See also:
C4eElement, C4E_ELEM_ASGN_MEM()
void c4e_poly_mul ( C4E_CONST C4eElement *C4E_RESTRICT  a,
C4E_CONST C4eElement *C4E_RESTRICT  b,
C4eElement *C4E_RESTRICT  c 
)

Multiplication of two binary polynomials (with coefficients in 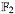$ \mathbb{F}_2$).

Note:
Because this function implements a kind of classical school book algorithm, it's complexity is O(a->size * b->size).
The parameters a and b have not to be normalized, except for performance reasons.
Precondition:
c->digits must point to pre-allocated memory space for at least (a->size + b->size) digits.
Use of restrict qualifier indicates that aliasing a or b with c or aliasing a->digits or b->digits with c->digits is not allowed.
Bibliography:
Peterson, W. Wesley und E. J. Weldon, Jr.: Error-Correcting Codes. MIT Press, 1972.
Bibliography:
Berlekamp, Elwyn R.: Algebraic Coding Theory. Aegean Park Press, 1984.
Parameters:
[in] a First multiplier (polynomial).
[in] b Second multiplier (polynomial).
[out] c Result 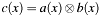$ c(x) = a(x) \otimes b(x) $, not normalized.
See also:
C4eElement, C4E_ELEM_ASGN_MEM()
void c4e_poly_sqr ( C4E_CONST C4eElement *  a,
C4eElement *  c 
)

Square of a binary polynomial (with coefficients in 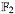$ \mathbb{F}_2$).

Note:
The algorithm has complexity O(a->size * a->size / 2).
The argument a has not to be normalized, except for performance reasons.
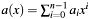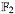The algorithm is based on $ a(x)=\sum_{i=0}^{n-1} a_i x^i $, and the following addition / multiplication rules in $ \mathbb{F}_2$:

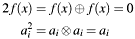
\begin{align*} 2 f(x) &= f(x) \oplus f(x) = 0\\ a_i^2 &= a_i \otimes a_i = a_i \end{align*}

Then this simplification is applicable:

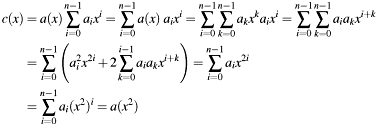
\begin{align*} c(x) &= a(x)\sum_{i=0}^{n-1} a_i x^i = \sum_{i=0}^{n-1} a(x)\; a_i x^i = \sum_{i=0}^{n-1} \sum_{k=0}^{n-1} a_k x^k a_i x^i = \sum_{i=0}^{n-1} \sum_{k=0}^{n-1} a_i a_k x^{i+k}\\ &= \sum_{i=0}^{n-1} \left(a_i^2 x^{2 i} + 2\sum_{k=0}^{i-1} a_i a_k x^{i+k} \right) = \sum_{i=0}^{n-1} a_i x^{2 i}\\ &= \sum_{i=0}^{n-1} a_i (x^2)^i = a(x^2) \end{align*}

Precondition:
c->digits must point to pre-allocated memory space for at least (2U * a->size) digits.
Parameters:
[in] a Polynomial 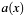$ a(x) $ to be squared.
[out] c Result 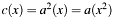$ c(x)=a^2(x)=a(x^2) $, not normalized. It is allowed to set c pointing to a resp. c->digits pointing to a->digits.
See also:
C4eElement, C4E_ELEM_ASGN_MEM()
void c4e_poly_mod ( C4E_CONST C4eElement *C4E_RESTRICT  a,
C4E_CONST C4eElement *C4E_RESTRICT  b,
C4E_CONST C4eElement *C4E_RESTRICT  m,
C4eElement *C4E_RESTRICT  c 
)

Modulo-division of two binary polynomials (reduction), with optional pre-multiplication by a third polynomial.

Note:
This function combines the multiplication algorithm in c4e_poly_mul() with a Linear Feedback Shift Register (LFSR) based division, according to [Peterson], figure 7.6. The algorithm is illustrated in [Peterson], figure 7.8.
The parameters a and b have not to be normalized, except for performance reasons.
Precondition:
The modulus m must be normalized, e.g. by using function c4e_elem_norm().
Divide by zero is not supported - catch this situation in advance (e.g. using macro C4E_ELEM_IS_ZERO(m)).
If factor b is used, then it's size must be less/equal m->size (in best-case it is also reduced to m).
c->digits must point to pre-allocated memory space for at least m->size digits.
Use of restrict qualifier indicates that aliasing a or b with c or aliasing a->digits or b->digits with c->digits is not allowed.
Bibliography:
Peterson, W. Wesley und E. J. Weldon, Jr.: Error-Correcting Codes. MIT Press, 1972.
Bibliography:
Berlekamp, Elwyn R.: Algebraic Coding Theory. Aegean Park Press, 1984.
Parameters:
[in] a First multiplier in dividend 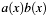$ a(x) b(x) $.
[in] b Second multiplier in 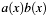$ a(x) b(x) $. If it is NULL, then 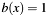$ b(x) = 1 $ is assumed. In the other case b is allowed to point to a or b->digits point to a->digits.
[in] m Divisor polynomial (modulus).
[out] c Result 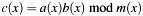$ c(x) = a(x) b(x) \bmod m(x) $, normalized.
See also:
C4eElement, C4E_ELEM_ASGN_MEM()
void c4e_poly_gcd ( C4eElemTriple *  a,
C4eElemTriple *  b 
)

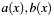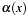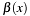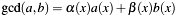Greatest Common Divisor of two binary polynomials $ a(x),b(x) $ over $ \mathbb{F}_2 $. It calculates the GCD of a->x and b->x together with the Bezout cofactors $ \alpha(x) $ and $ \beta(x) $ in equation $ \gcd(a,b)=\alpha(x) a(x) + \beta(x) b(x) $.

Note:
The asymptotic complexity of the algorithm is O(a->x.size * b->x.size).
If 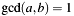$ \gcd(a,b)=1 $ the algorithm computes 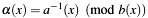$ \alpha(x) = a^{-1}(x) \pmod{b(x)} $ in a->y and returns a->x in a->z, b->x in b->z.
Members a->attr and b->attr have no meaning (will be destroyed).
Precondition:
The polynomials a->x and b->x must be normalized, e.g. by using function c4e_elem_norm().
It is not allowed that both polynomials a->x and b->x are both zero (C4E_ELEM_IS_ZERO()).
The required digits space (in units of C4eArchDigit) for all polynomials is the maximum size of the two input values a->x and b->x + 1U.
Bibliography:
Menezes, Alfred J., P. C. van Oorschot und Scott A. Vanstone: Handbook of applied cryptography. CRC Press Series on Discrete Mathematics and Its Application. CRC Press, 2. Edition, 1992.
Bibliography:
Hankerson, Darrel, Alfred Menezes und Scott Vanstone: Guide to Elliptic Curve Cryptography. Springer, New York, 2004.
Bibliography:
Crandall, Richard und Carl Pomerance: Prime Numbers. A Computational Perspective. Springer, 2. Auflage, 2005.
Bibliography:
Berlekamp, Elwyn R.: Algebraic Coding Theory, Revised 1984 Edition. Aegean Park Press, Laguna Hills, CA, 1984.
Parameters:
[in,out] a As an input parameter a->x holds the polynomial, for which the GCD with b->x is calculated. As an output it returns:

  • zero in a->x;
  • the coprime part of a->x in a->z;
  • Bezout cofactor 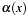$ \alpha(x) $ in a->y.
[in,out] b As an input parameter b->x holds the polynomial, for which the GCD with a->x is calculated. As an output it returns:

  • the 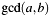$ \gcd(a,b) $ in b->x;
  • the coprime part of b->x in b->z;
  • Bezout cofactor 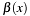$ \beta(x) $ in b->y.
See also:
C4eElemTriple, c4e_elem_norm(), C4E_ELEM_IS_ZERO(), C4eElement, C4E_ELEM_ASGN_MEM()
Generated by Ralf Hoppe, Ginsterweg 49, 73230 Kirchheim unter Teck, Germany
on Sun Jun 7 14:10:51 2015 for CRY4E using doxygen 1.6.1