c4e_modn.h File Reference
(Version 579)
Modular arithmetic in ring  .
More...
.
More...
#include "c4e_bigint.h"
Go to the source code of this file.
Defines | |
| #define | C4E_MODN_POW_SPACE(msize) |
| Size calculation macro for modular exponentiation parameters size (in units of C4eArchDigit). | |
Functions | |
| void | c4e_modn_pow (C4eElement *C4E_RESTRICT a, C4E_CONST C4eElement *C4E_RESTRICT n, C4eElement *C4E_RESTRICT m, C4eElement *C4E_RESTRICT tmp, C4eElement *c) |
Power 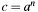 in in  , means , means 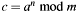 . . | |
| void | c4e_modn_crt (C4eElemTriple *C4E_RESTRICT p, C4eElemTriple *C4E_RESTRICT q) |
| Chinese Remainder Theorem (CRT). | |
Detailed Description
Modular arithmetic in ring  .
.
- Version:
- Id
- c4e_modn.h 579 2015-05-24 18:00:40Z ralf
Definition in file c4e_modn.h.
Define Documentation
| #define C4E_MODN_POW_SPACE | ( | msize | ) |
Size calculation macro for modular exponentiation parameters size (in units of C4eArchDigit).
- Parameters:
-
[in] msize Size of modulus in units of C4eArchDigit.
- Returns:
- Required digit space (in units of C4eArchDigit) when using c4e_modn_pow() or functions based on it.
Definition at line 47 of file c4e_modn.h.
Function Documentation
| void c4e_modn_pow | ( | C4eElement *C4E_RESTRICT | a, | |
| C4E_CONST C4eElement *C4E_RESTRICT | n, | |||
| C4eElement *C4E_RESTRICT | m, | |||
| C4eElement *C4E_RESTRICT | tmp, | |||
| C4eElement * | c | |||
| ) |
Power 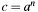 in
in  , means
, means 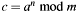 .
.
The implemented left-to-right algorithm is based on the binary representation of exponent 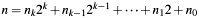 , which gives:
, which gives:
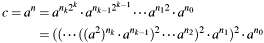
- Note:
- If modulus
mis odd, it uses Montgomery's algorithm. -
This algorithm has an asymptotic complexity of about
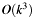 , if
, if 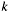 also designates the size of modulus
also designates the size of modulus m.
- Attention:
- The modulus
mis temporary modified - so it must be writable. After function return it holds the same values as at function entry.
- Precondition:
- It is not allowed that both numbers
aandnare zero. The caller has to ensure this, may be using macro C4E_ELEM_IS_ZERO(). -
The required digits space (in units of C4eArchDigit) for
ais (m->size+ 1). The space fortmp->digitsandc->digitsisC4E_MODN_POW_SPACE(m->size), but only ifmis odd (Montgomery algorithm). In casemis even, the required digits space fortmp->digitsandc->digitsis (2U *m->size) digits. -
The parameters
mandamust be normalized, for example using function c4e_elem_norm(). -
Parameter
amust be reduced tomon entry. Use for example function c4e_bigint_mod() to ensure this.
- Bibliography:
- Montgomery, P.: Modular multiplication without trial division. Mathematics of Computation, 44(170):519-521, 1985.
- Bibliography:
- Koc, Cetin Kaya, Tolga Acar and Burton S. Kaliski, Jr.: Analyzing and Comparing Montgomery Multiplication Algorithms. IEEE Micro, 16(3):26-33, Juni 1996.
- Bibliography:
- Burton S. Kaliski: The Montgomery Inverse and Its Applications IEEE Transactions on Computers, 44(8):1064-1065, August 1995.
- Parameters:
-
[in] a Big number ain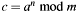 . Notice that number
. Notice that number ais destroyed.[in] n Exponent nin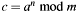 .
. [in] m Modulus (greater than zero), temporary modified. tmp Temporary space needed for intermediate results. [out] c Result cin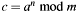 , normalized.
, normalized.
| void c4e_modn_crt | ( | C4eElemTriple *C4E_RESTRICT | p, | |
| C4eElemTriple *C4E_RESTRICT | q | |||
| ) |
Chinese Remainder Theorem (CRT).
The Chinese Remainder Theorem can be used to solve linear congruences of the form:
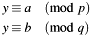
under the precondition that p and q are coprime (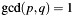 ). Typically the CRT is given in the literature by the following formula:
). Typically the CRT is given in the literature by the following formula:
![\[ y = \alpha b p + \beta a q + kpq, \qquad k \in \mathbb{Z} \]](form_125.png)
which is closely related to the extended GCD algorithm and Bezout's theorem: 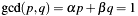 . The implemented algorithm uses a variant introduced by H.L. Garner:
. The implemented algorithm uses a variant introduced by H.L. Garner:
![\begin{align*} y &= a + \alpha p (b-a) + kpq, \qquad k \in \mathbb{Z} \\ y &= a + p [\alpha (b-a) \bmod q], \qquad 0 \leq y < pq \end{align*}](form_127.png)
Notice that in this form the Bezout cofactor 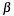 is not needed - so
is not needed - so q->y is used (internally) for intermediate calculations.
- Bibliography:
- Koc, Cetin Kaya: High-Speed RSA Implementation. Technical Report TR-201, RSA Laboratories, 1994. Version 2.0
- Bibliography:
- Garner, Harvey L.: The Residue Number System. IRE Transactions on Electronic Computers, 8(2):140-147, Juni 1959.
- Note:
- Internally, if the result of
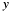 is negative the algorithm adds
is negative the algorithm adds 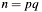 once to the result, which so becomes positive. Therefore result
once to the result, which so becomes positive. Therefore result 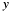 is always positive and less than
is always positive and less than 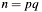 . In consequence the members
. In consequence the members p->attrandq->attrhave no meaning as return parameters.
- Precondition:
- Numbers
p->xresp.q->xmust be less than the associated modulusp->zresp.q->z. -
All input parameters referenced via
pandq, that are big numbers must be normalized, for example using function c4e_elem_norm(). -
The caller hast to ensure that numbers
p->zandq->zare relatively prime, else the algorithm does produce a wrong result. -
The caller must provide at least the following digits space (each digit of size
C4E_ARCH_DIGIT_SIZE):p->z.size+ q->z.size + 1 forp->xandq->x;- 2 *
q->z.sizeforq->x, if that is greater thanp->z.size+ q->z.size + 1; p->x.sizeforq->y.
- Parameters:
-
[in,out] p Input parameters of first (modular) congruence 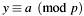 resp. first summand in Bezout's theorem
resp. first summand in Bezout's theorem 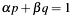 and return value
and return value 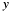 :
:
- modulus
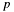 in
in p->z(unchanged); - cofactor
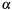 in
in p->y(unchanged); - sign of cofactor
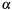 in
in p->attr; - number
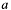 in
in p->x. At function return memberp->xholds the (positive) result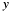 .
.
[in,out] q Input parameters of second (modular) congruence resp. first summand in Bezout's theorem and return value 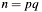 :
:
- modulus
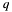 in
in q->z(unchanged); - temporary used memory space in
q->yandq->attr(destroyed); - number
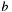 in
in q->x. At function return memberq->xholds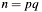 .
.
- modulus
- See also:
- C4eElemTriple, c4e_bigint_gcd(), C4E_ELEM_ASGN_MEM()
 1.6.1
1.6.1