c4e_mod2n.h File Reference
(Version 551)
Modular (polynomial) arithmetic in ring ![$ \mathbb{Z}_2[x] / m(x) $](form_107.png) .
More...
.
More...
#include "c4e_poly.h"
Include dependency graph for c4e_mod2n.h:
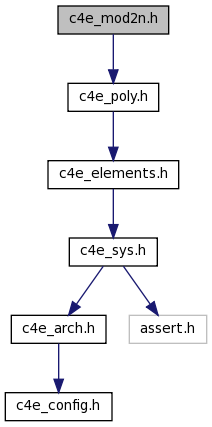
Go to the source code of this file.
Functions | |
| void | c4e_mod2n_sqr (C4E_CONST C4eElement *C4E_RESTRICT a, C4E_CONST C4eElement *C4E_RESTRICT m, C4eElement *C4E_RESTRICT c) |
Square of a binary polynomial (having coefficients from 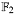 ), with modular reduction. ), with modular reduction. | |
| void | c4e_mod2n_pow (C4E_CONST C4eElement *C4E_RESTRICT a, C4E_CONST C4eElement *C4E_RESTRICT n, C4E_CONST C4eElement *C4E_RESTRICT m, C4eElement *C4E_RESTRICT tmp, C4eElement *c) |
Modulo-power 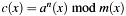 of a binary polynomial (with coefficients in of a binary polynomial (with coefficients in 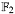 ). ). | |
Detailed Description
Modular (polynomial) arithmetic in ring ![$ \mathbb{Z}_2[x] / m(x) $](form_107.png) .
.
- Note:
- This interface is the counterpart to c4e_modn.h.
- Version:
- Id
- c4e_mod2n.h 551 2015-03-01 12:37:45Z ralf
Definition in file c4e_mod2n.h.
Function Documentation
| void c4e_mod2n_sqr | ( | C4E_CONST C4eElement *C4E_RESTRICT | a, | |
| C4E_CONST C4eElement *C4E_RESTRICT | m, | |||
| C4eElement *C4E_RESTRICT | c | |||
| ) |
Square of a binary polynomial (having coefficients from 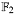 ), with modular reduction.
), with modular reduction.
- Note:
- The algorithm has complexity O(
a->size^ 2).
- Precondition:
- The size of argument
aMUST be less/equalm->size, but not to be normalized (except for performance reasons). -
c->digitsmust point to pre-allocated memory space for at leastm->sizedigits. -
Use of restrict qualifier indicates that aliasing
awithcor aliasinga->digitswithc->digitsis not allowed.
- Parameters:
-
[in] a Polynomial 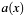 to be squared.
to be squared. [in] m Modulus (binary polynomial), unequal to zero. [out] c Result 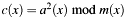 , not normalized.
, not normalized.
- See also:
- C4eElement, C4E_ELEM_ASGN_MEM()
| void c4e_mod2n_pow | ( | C4E_CONST C4eElement *C4E_RESTRICT | a, | |
| C4E_CONST C4eElement *C4E_RESTRICT | n, | |||
| C4E_CONST C4eElement *C4E_RESTRICT | m, | |||
| C4eElement *C4E_RESTRICT | tmp, | |||
| C4eElement * | c | |||
| ) |
Modulo-power 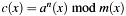 of a binary polynomial (with coefficients in
of a binary polynomial (with coefficients in 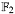 ).
).
The algebraic operation performed by this left-to-right algorithm is a (modular) exponentiation in finite field 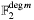 . It is based on the binary representation of exponent
. It is based on the binary representation of exponent 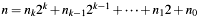 , which results in:
, which results in:
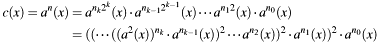
- Note:
- The parameters
aandnshould be normalized, because of performance reasons. -
Parameter
ashould be reduced tomon function entry, for example using c4e_poly_mod(a_in, NULL, m, a_out).
- Precondition:
- It is not allowed that both
a(x)andnare zero. The caller has to ensure this, may be using macro C4E_ELEM_IS_ZERO(). -
c->digitsandtmp->digitsmust point to pre-allocated memory space for at leastm->sizedigits. -
The parameter
mmust be normalized, for example using function c4e_elem_norm(). - Use of restrict qualifier indicates that aliasing any of the argument pointers with the result pointer is not allowed.
- Parameters:
-
[in] a Argument (binary polynomial). [in] n Big number exponent. [in] m Modulus (binary polynomial), unequal to zero. tmp Temporary space needed for intermediate results. [out] c Result 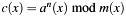 , not normalized.
, not normalized.
 1.6.1
1.6.1