EC Diffie-Hellman (ECDH) over binary fields
[ECC over binary field]

Diffie-Hellman shared secret computation in elliptic curve (EC) domain over binary field . More...

Functions
C4eArchSize	c4e_ecc2n_dh (C4E_CONST C4eEcDomain *C4E_RESTRICT dom, C4E_CONST C4eElement *C4E_RESTRICT d, C4E_CONST C4eEcPoint *C4E_RESTRICT q, C4eArchDigit tmp[C4E_RESTRICT], C4eArchUint8 *C4E_RESTRICT secret)
	Elliptic Curve Diffie-Hellman (ECDH) over binary field shared secret computation (according to IEEE Std 1363, ECSVDP-DH or ECSVDP-DHC primitive and ANSI X9.63).

---

Detailed Description

Diffie-Hellman shared secret computation in elliptic curve (EC) domain over binary field .

---

Function Documentation

C4eArchSize c4e_ecc2n_dh	(	C4E_CONST C4eEcDomain *C4E_RESTRICT	dom,
		C4E_CONST C4eElement *C4E_RESTRICT	d,
		C4E_CONST C4eEcPoint *C4E_RESTRICT	q,
		C4eArchDigit	tmp[C4E_RESTRICT],
		C4eArchUint8 *C4E_RESTRICT	secret
	)

Elliptic Curve Diffie-Hellman (ECDH) over binary field shared secret computation (according to IEEE Std 1363, ECSVDP-DH or ECSVDP-DHC primitive and ANSI X9.63).

This function performs an EC point (the others party public key q) multiplication with the own private key (which is big number d). If cofactor dom->h is unequal to zero (see C4E_ELEM_IS_ZERO()) and unequal to one (see C4E_ELEM_IS_ONE()) then d is pre-multiplied with the cofactor dom->h, realizing the ECDHC algorithm. The x-coordinate of the resulting point 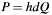is the shared secret. This is conforming to ANSI X9.63, section 5.4 and IEEE Std 1363, section 7.2.2.

Note:

The ordinary ECDH algorithm is widely in use but a little obsolete, because of some known attacks against small cofactors. Therefore standards like ANSI X9.63 and NIST SP800-56A do not include this algorithm - instead they specify the Cofactor Elliptic Curve Diffie-Hellman (ECDHC) algorithm.

Precondition:

The validity of the EC domain parameters in dom must be assured by the caller, either implicit or by using function c4e_ecc2n_domchk().

The validity of the private ECDH key d must be assured by the caller, either implicit or by using function c4e_ecc2n_keychk_prv().

The validity of the public ECDH key must be assured by the caller, for example by using function c4e_ecc2n_keychk_pub().

The caller must provide temporary memory space in array tmp[], using macro C4E_ECC2N_TMP_NUM() in conjunction with temp. space qualifier C4E_ECC2N_DH_TMPID_ORD or C4E_ECC2N_DH_TMPID_COF (depending on the value dom->h).

Bibliography:

Standard Specifications For Public-Key Cryptography. Std 1363-2000, IEEE, 2000.

Bibliography:

Public Key Cryptography For The Financial Services Industry: Key Agreement and Key Transport Using Elliptic Curve Cryptography. ANSI X9.63, 2001.

Bibliography:

Standards for Efficient Cryptography Group - SEC 1: Elliptic Curve Cryptography. Certicom Research. 2000.

Parameters:

[in]	dom	Pointer to ECC2N domain parameters.
[in]	d	Pointer to ECDH private key, which is a big number.
[in]	q	Other party ECDH public key (curve point).
	tmp	Array of temporary space elements (see preconditions for details on size).
[out]	secret	Shared secret of both parties, in network byte order.

Returns:

The length of shared secret (typically dom->m.len), 0 on error.

See also:

c4e_ecc2n_keychk_prv(), c4e_ecc2n_keychk_pub(), c4e_ecc2n_domchk(), C4E_ECC2N_DH_TMPID_ORD, C4E_ECC2N_DH_TMPID_COF