ECC over binary field
[Elliptic Curve Cryptography (ECC)]

Modules

 Binary Field EC Temp. Space Qualifiers
 

Temp. space qualifiers for EC based cryptography over binary field.


 EC Diffie-Hellman (ECDH) over binary fields
 

Diffie-Hellman shared secret computation in elliptic curve (EC) domain over binary field $ \mathbb{F}_{2^n} $.


 Elliptic Curve Digital Signature Algorithm (ECDSA)
 

Elliptic Curve Digital Signature Algorithm (ECDSA).


Functions

C4eSysStatus c4e_ecc2n_domchk (C4eArchUint algos, C4E_CONST C4eEcDomain *dom, C4eArchDigit *C4E_RESTRICT tmp)
 A simple (and fast) domain parameter validity test for elliptic curves over binary field $ \mathbb{F}_{2^n} $.
C4eSysStatus c4e_ecc2n_keychk_prv (C4eArchUint algos, C4E_CONST C4eEcDomain *C4E_RESTRICT dom, C4E_CONST C4eElement *C4E_RESTRICT d, C4eArchDigit tmp[C4E_RESTRICT])
 Elliptic curve (EC) over binary field $ \mathbb{F}_{2^n} $ private key validity test.
C4eSysStatus c4e_ecc2n_keychk_pub (C4eArchUint algos, C4E_CONST C4eEcDomain *C4E_RESTRICT dom, C4E_CONST C4eEcPoint *C4E_RESTRICT q, C4eArchDigit tmp[C4E_RESTRICT])
 Elliptic curve (EC) over binary field $ \mathbb{F}_{2^n} $ public key validity test.
C4eArchSize c4e_ecc2n_pt2os (C4E_CONST C4eEcDomain *C4E_RESTRICT dom, C4E_CONST C4eEcPoint *C4E_RESTRICT pt, C4eArchUint ptfmt, C4eArchDigit tmp[C4E_RESTRICT], C4eArchSize bufsize, C4eArchUint8 *C4E_RESTRICT buf)
 Elliptic curve point to octet string conversion primitive, according to ANSI X9.63, section 4.3.6 and 4.2.2 and IEEE Std 1363, section A.9.6 and annex E.2.3.
C4eSysStatus c4e_ecc2n_os2pt (C4E_CONST C4eEcDomain *C4E_RESTRICT dom, C4E_CONST C4eArchUint8 *C4E_RESTRICT osp, C4eArchSize len, C4eArchDigit tmp[C4E_RESTRICT], C4eEcPoint *C4E_RESTRICT pt)
 Octet string to elliptic curve point conversion primitive, according to ANSI X9.63, section 4.3.7 and 4.2.2 and IEEE Std 1363, section A.9.6 and annex E.2.3.

Binary Field ECC Algorithm Identifiers

Algorithm identifiers for ECC over binary field $ \mathbb{F}_{2^n} $, to be used as parameter to c4e_ecc2n_domchk().



#define C4E_ECC2N_ALGO_NONE
 "unspecific" algorithm identifier.
#define C4E_ECC2N_ALGO_DH
 ECDH algorithm identifier.
#define C4E_ECC2N_ALGO_DSA
 ECDSA algorithm identifier.
#define C4E_ECC2N_ALGO_ALL
 "all" algorithm identifier.

Function Documentation

C4eSysStatus c4e_ecc2n_domchk ( C4eArchUint  algos,
C4E_CONST C4eEcDomain *  dom,
C4eArchDigit *C4E_RESTRICT  tmp 
)

A simple (and fast) domain parameter validity test for elliptic curves over binary field $ \mathbb{F}_{2^n} $.

Function c4e_ecc2n_domchk() checks the following conditions:

  1. The modulus dom->m.val must not be m(x) = 0, not m(x) = 1 and must not have a common (polynomial) factor x.
  2. The size of modulus dom->m.val must be less/equal than C4E_ELEM_DIGITS_NUM(dom->m.len).
  3. The field size dom->m.len must be less/equal C4E_EC_GF_BYTES_MAX (if defined).
  4. Curve parameters dom->a and dom->b must be less than dom->m.val.
  5. Curve parameter dom->b must not be zero (dom->a is allowed to be zero, then elliptic curve E is a Koblitz curve).
  6. The order of base point G in dom->q.val must be greater than zero and odd (because #G must be a prime number).
  7. The number of digits in dom->q.val must be less than the equivalent value derived from dom->q.len.
  8. The number of digits in dom->q.val must be less than the maximum group order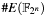 $ \#E(\mathbb{F}_{2^n}) $ of elliptic curve E (see C4E_EC_FIELD_DIGITS_MAX).
  9. The cofactor dom->h must be less than dom->q (only if bit C4E_ECC2N_ALGO_DH set in algos).
  10. The coordinate values of base point G are in range of underlying ground field $ \mathbb{F}_{2^n} $ (only if bit C4E_ECC2N_ALGO_DSA set in algos).
  11. The base point G is a field element of elliptic curve E and it is really a base point, satisfying the condition 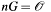$ nG=\mathcal{O} $ (but only if tmp is unequal to NULL and bit C4E_ECC2N_ALGO_DSA set in algos).

So this function is able to check conditions #1, #2, #4, #5 and #7 of ANSI X9.62 section 5.1.2.2.

Note:
In field $ \mathbb{F}_{2^n} $ the size of irreducible polynomial m(x) is one bit larger than the maximum size of each field element. Because we do not know the maximum size of a field element in bits (we only know it in bytes) we allow a size for m(x) which is one bit greater than (dom->m.len * 8) bits.
Precondition:
The caller may provide temporary memory space in array tmp[], using macro C4E_ECC2N_TMP_NUM() in conjunction with temp. space qualifier C4E_ECC2N_TMPID_DOM_CHECK. Currently this is needed only if C4E_ECC2N_ALGO_DSA is set in algos and the base point G must be validated by extended test (see last point of description).
Bibliography:
Standard Specifications For Public-Key Cryptography. Std 1363-2000, IEEE, 2000.
Bibliography:
Public Key Cryptography For The Financial Services Industry: The Elliptic Curve Digital Signature Algorithm (ECDSA). ANSI X9.62, 1998.
Bibliography:
Public Key Cryptography For The Financial Services Industry: Key Agreement and Key Transport Using Elliptic Curve Cryptography. ANSI X9.63, 2001.
Parameters:
[in] algos Algorithm identifiers to check domain parameters for (or'ed together).
[in] dom Pointer to domain parameters.
tmp Array of temporary space elements (see preconditions for details on size). Currently parameter tmp is allowed to be NULL if C4E_ECC2N_ALGO_DSA is not set in algos or the extended test should not be performed.
Returns:
Validity status of dom.
Return values:
C4E_STATUS_OK If the domain parameters are usable for all calculations (valid in the sense of this implementation).
other If one of the domain parameters is invalid.
See also:
C4eEcDomain
Todo:
If CRY4E supports key generation (may be in the future) then implement additional tests according to IEEE Std 1363, annex A.16.8 and ANSI X9.63, section 5.1.2.2.
C4eSysStatus c4e_ecc2n_keychk_prv ( C4eArchUint  algos,
C4E_CONST C4eEcDomain *C4E_RESTRICT  dom,
C4E_CONST C4eElement *C4E_RESTRICT  d,
C4eArchDigit  tmp[C4E_RESTRICT] 
)

Elliptic curve (EC) over binary field $ \mathbb{F}_{2^n} $ private key validity test.

The function validates parameter d with respect to:

  • the allowed range: $ 0 < d < \#G $.
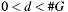Precondition:
The validity of the EC domain parameters in dom must be assured by the caller, either implicit or by using function c4e_ecc2n_domchk().
All binary polynomials in dom must be normalized, e.g. by using functions c4e_elem_norm(), c4e_elem_os2e() and/or c4e_ecc2n_os2pt().
The private key d, which is a big number, must be normalized, e.g. by using functions c4e_elem_norm() or c4e_elem_os2e().
Bibliography:
Standard Specifications For Public-Key Cryptography. Std 1363-2000, IEEE, 2000.
Bibliography:
Public Key Cryptography For The Financial Services Industry: Key Agreement and Key Transport Using Elliptic Curve Cryptography. ANSI X9.63, 2001.
Parameters:
[in] algos Algorithm identifiers to check the private key for (or'ed together).
[in] dom Pointer to EC domain parameters.
[in] d Private EC key (a big number) to be tested.
tmp Array of temporary space elements (unused at the moment).
Returns:
Validity status of d.
Return values:
C4E_STATUS_OK If the key seems to be valid.
other If the key is invalid.
See also:
C4eEcDomain, C4eElement
C4eSysStatus c4e_ecc2n_keychk_pub ( C4eArchUint  algos,
C4E_CONST C4eEcDomain *C4E_RESTRICT  dom,
C4E_CONST C4eEcPoint *C4E_RESTRICT  q,
C4eArchDigit  tmp[C4E_RESTRICT] 
)

Elliptic curve (EC) over binary field $ \mathbb{F}_{2^n} $ public key validity test.

Note:
This function is fully conforming to the "Embedded Public Key Validation Primitive" in ANSI X9.63, section 5.2.2.2 and the simple public key validation test according to IEEE Std 1363, section A.16.10.
Precondition:
The validity of the EC domain parameters in dom must be assured by the caller, either implicit or by using function c4e_ecc2n_domchk().
All binary polynomials in q and dom must be normalized, e.g. by using functions c4e_elem_norm(), c4e_elem_os2e() and/or c4e_ecc2n_os2pt().
The caller may provide temporary memory space in array tmp[], using macro C4E_ECC2N_TMP_NUM() in conjunction with temp. space qualifier C4E_ECC2N_TMPID_KEY_CHECK.
Bibliography:
Standard Specifications For Public-Key Cryptography. Std 1363-2000, IEEE, 2000.
Bibliography:
Public Key Cryptography For The Financial Services Industry: The Elliptic Curve Digital Signature Algorithm (ECDSA). ANSI X9.62, 1998.
Bibliography:
Public Key Cryptography For The Financial Services Industry: Key Agreement and Key Transport Using Elliptic Curve Cryptography. ANSI X9.63, 2001.
Parameters:
[in] algos Algorithm identifiers to check the public key for (or'ed together).
[in] dom Pointer to EC domain parameters.
[in] q Public EC key to be tested.
tmp Array of temporary space elements (see preconditions for details on size).
Returns:
Validity status of key.
Return values:
C4E_STATUS_OK If the key seems to be valid.
other If the key is invalid.
See also:
C4eEcDomain, C4eEcPoint, c4e_ecc2n_domchk()
Todo:
If CRY4E supports key generation (may be in the future) then implement additional tests according to IEEE Std 1363, annex A.16.8 and ANSI X9.63, section 5.1.2.2.
C4eArchSize c4e_ecc2n_pt2os ( C4E_CONST C4eEcDomain *C4E_RESTRICT  dom,
C4E_CONST C4eEcPoint *C4E_RESTRICT  pt,
C4eArchUint  ptfmt,
C4eArchDigit  tmp[C4E_RESTRICT],
C4eArchSize  bufsize,
C4eArchUint8 *C4E_RESTRICT  buf 
)

Elliptic curve point to octet string conversion primitive, according to ANSI X9.63, section 4.3.6 and 4.2.2 and IEEE Std 1363, section A.9.6 and annex E.2.3.

Precondition:
The validity of the EC domain parameters in dom must be assured by the caller, either implicit or by using function c4e_ecc2n_domchk().
All binary polynomials in pt and dom must be normalized, e.g. by using functions c4e_elem_norm(), c4e_elem_os2e() and/or c4e_ecc2n_os2pt().
All polynomials in pt and dom must be normalized, e.g. by using functions c4e_elem_norm() or c4e_elem_os2e().
The function does not handle the pseudo-point at infinity. Use for example C4E_EC_IS_ZERO() to detect this situation in advance.
The caller must provide temporary memory space in array tmp[], using macro C4E_ECC2N_TMP_NUM() in conjunction with temp. space qualifier C4E_ECC2N_TMPID_PT2OS.
The minimum required buffer size (in bytes) for buf varies depending the point format ptfmt: * hybrid: 2U * dom->m.len + 1U * uncompressed: 2U * dom->m.len + 1U * compressed: dom->m.len + 1U
Bibliography:
Public Key Cryptography For The Financial Services Industry: Key Agreement and Key Transport Using Elliptic Curve Cryptography. ANSI X9.63, 2001.
Bibliography:
Standard Specifications For Public-Key Cryptography. Std 1363-2000, IEEE, 2000.
Parameters:
[in] dom Pointer to EC domain parameters.
[in] pt Pointer to EC point.
[in] ptfmt EC point format: * C4E_EC_PTFMT_PC_C: compressed * C4E_EC_PTFMT_PC_U: uncompressed * C4E_EC_PTFMT_PC_H: hybrid
tmp Array of temporary space elements (see preconditions for details on size). Parameter tmp may be NULL in case the format is pure "uncompressed".
[in] bufsize Maximum number of bytes to store in buf (must be greater than zero, else an assert is thrown).
[out] buf Output buffer, getting converted EC point pt.
Returns:
Number of bytes to represent pt, 0 on error.
C4eSysStatus c4e_ecc2n_os2pt ( C4E_CONST C4eEcDomain *C4E_RESTRICT  dom,
C4E_CONST C4eArchUint8 *C4E_RESTRICT  osp,
C4eArchSize  len,
C4eArchDigit  tmp[C4E_RESTRICT],
C4eEcPoint *C4E_RESTRICT  pt 
)

Octet string to elliptic curve point conversion primitive, according to ANSI X9.63, section 4.3.7 and 4.2.2 and IEEE Std 1363, section A.9.6 and annex E.2.3.

Note:
This function cannot convert the pseudo-point at infinity (returns C4E_STATUS_ECODING in that case).
Precondition:
The validity of the EC domain parameters in dom must be assured by the caller, either implicit or by using function c4e_ecc2n_domchk().
All binary polynomials in dom must be normalized, e.g. by using functions c4e_elem_norm() or c4e_elem_os2e().
The caller must provide temporary memory space in array tmp[], using macro C4E_ECC2N_TMP_NUM() in conjunction with temp. space qualifier C4E_ECC2N_TMPID_OS2PT.
The size of buffers pt->x.digits respective pt->y.digits (in number of digits according to pt->x.size respective pt->y.size) must be at least: 
 C4E_ELEM_DIGITS_NUM(dom->m.len)
or, when using (maximum) static memory reservation: 
 C4E_ELEM_DIGITS_NUM(C4E_EC_GF_BYTES_MAX)
Postcondition:
The coordinate values pt->x and pt->y are normalized.
Bibliography:
Public Key Cryptography For The Financial Services Industry: Key Agreement and Key Transport Using Elliptic Curve Cryptography. ANSI X9.63, 2001.
Bibliography:
Standard Specifications For Public-Key Cryptography. Std 1363-2000, IEEE, 2000.
Parameters:
[in] dom Pointer to EC domain parameters.
[in] osp Octet string pointer, which represents an EC point, according to the standards mentioned.
[in] len Number of bytes in osp array (octet string).
tmp Array of temporary space elements (see preconditions for details on size).
[out] pt Pointer to EC point, with coordinate digits buffer prepared according to preconditions.
Returns:
Conversion result.
Return values:
C4E_STATUS_OK If the octet string was converted successfully.
other If conversion of octet string has failed.
See also:
C4eEcDomain, C4eEcPoint, C4eElement, C4E_ELEM_ASGN_MEM()
Generated by Ralf Hoppe, Ginsterweg 49, 73230 Kirchheim unter Teck, Germany
on Sun Jun 7 14:10:51 2015 for CRY4E using doxygen 1.6.1