c4e_ecgf2n.h File Reference
(Version 573)
Elliptic curve (EC) arithmetic over  .
More...
.
More...
#include "c4e_ec.h"#include "c4e_gf2n.h"
Go to the source code of this file.
Functions | |
| void | c4e_ecgf2n_cpy (C4E_CONST C4eEcPoint *C4E_RESTRICT src, C4eEcPoint *C4E_RESTRICT dst) |
| Copies an elliptic curve point. | |
| void | c4e_ecgf2n_neg (C4E_CONST C4eEcPoint *C4E_RESTRICT pt, C4eEcPoint *C4E_RESTRICT pt3) |
Negative point on an elliptic curve 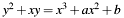 over the binary field over the binary field  . . | |
| C4eSysStatus | c4e_ecgf2n_add (C4E_CONST C4eEcDomain *C4E_RESTRICT dom, C4E_CONST C4eEcPoint *C4E_RESTRICT pt1, C4E_CONST C4eEcPoint *C4E_RESTRICT pt2, C4eArchDigit tmp[C4E_RESTRICT], C4eEcPoint *C4E_RESTRICT pt3) |
Addition of two points on an elliptic curve 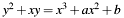 over the binary field over the binary field  . . | |
| C4eSysStatus | c4e_ecgf2n_dbl (C4E_CONST C4eEcDomain *C4E_RESTRICT dom, C4E_CONST C4eEcPoint *C4E_RESTRICT pt, C4eArchDigit tmp[C4E_RESTRICT], C4eEcPoint *C4E_RESTRICT pt3) |
Point doubling on an elliptic curve 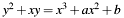 over the binary field over the binary field  . . | |
| C4eSysStatus | c4e_ecgf2n_mul (C4E_CONST C4eEcDomain *C4E_RESTRICT dom, C4E_CONST C4eElement *C4E_RESTRICT k, C4E_CONST C4eEcPoint *C4E_RESTRICT pt, C4eArchDigit tmp[C4E_RESTRICT], C4eEcPoint *C4E_RESTRICT kp) |
Point multiplication kP on an elliptic curve 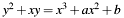 over the binary field over the binary field  . . | |
| C4eSysBool | c4e_ecgf2n_sign (C4E_CONST C4eEcDomain *C4E_RESTRICT dom, C4E_CONST C4eEcPoint *C4E_RESTRICT pt, C4eArchDigit tmp[C4E_RESTRICT]) |
Returns the "sign" of coordinate 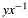 for an elliptic curve point over binary field for an elliptic curve point over binary field  , according to IEEE Std 1363, annex A.9.6. , according to IEEE Std 1363, annex A.9.6. | |
| C4eSysStatus | c4e_ecgf2n_gety (C4E_CONST C4eEcDomain *C4E_RESTRICT dom, C4eSysBool sign, C4eArchDigit tmp[C4E_RESTRICT], C4eEcPoint *C4E_RESTRICT pt) |
Calculates the y-coordinate associated with a x-coordinate for an elliptic curve over binary field  , according to IEEE Std 1363, annex A.12.9 and X9.62, section 4.2.2. , according to IEEE Std 1363, annex A.12.9 and X9.62, section 4.2.2. | |
| C4eSysStatus | c4e_ecgf2n_validate (C4E_CONST C4eEcDomain *C4E_RESTRICT dom, C4E_CONST C4eEcPoint *C4E_RESTRICT pt, C4eArchDigit tmp[C4E_RESTRICT]) |
Validates the coordinate values of an elliptic curve point are in range (fast) and optional verifies the point really is located on the elliptic curve over  . . | |
Detailed Description
Elliptic curve (EC) arithmetic over  .
.
- Note:
- This interface is the counterpart to c4e_ecp.h.
- Version:
- Id
- c4e_ecgf2n.h 573 2015-05-24 11:10:17Z ralf
Definition in file c4e_ecgf2n.h.
Function Documentation
| void c4e_ecgf2n_cpy | ( | C4E_CONST C4eEcPoint *C4E_RESTRICT | src, | |
| C4eEcPoint *C4E_RESTRICT | dst | |||
| ) |
Copies an elliptic curve point.
- Parameters:
-
[out] dst Pointer to destination point, which must have dst->x.digitsanddst->y.digitsset.[in] src Pointer to source point.
- See also:
- C4eEcPoint, C4E_ELEM_ASGN_MEM()
| void c4e_ecgf2n_neg | ( | C4E_CONST C4eEcPoint *C4E_RESTRICT | pt, | |
| C4eEcPoint *C4E_RESTRICT | pt3 | |||
| ) |
Negative point on an elliptic curve 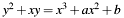 over the binary field
over the binary field  .
.
The algorithm calculates (according to IEEE Std 1363, annex A.10.2): 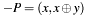 .
.
- Bibliography:
- Standard Specifications For Public-Key Cryptography. Std 1363-2000, IEEE, 2000.
- Bibliography:
- Hankerson, Darrel, Alfred Menezes und Scott Vanstone: Guide to Elliptic Curve Cryptography. Springer, New York, 2004.
- Parameters:
-
[in] pt Pointer to EC point 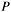 .
. [out] pt3 Resulting EC point 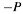 , normalized.
, normalized.
| C4eSysStatus c4e_ecgf2n_add | ( | C4E_CONST C4eEcDomain *C4E_RESTRICT | dom, | |
| C4E_CONST C4eEcPoint *C4E_RESTRICT | pt1, | |||
| C4E_CONST C4eEcPoint *C4E_RESTRICT | pt2, | |||
| C4eArchDigit | tmp[C4E_RESTRICT], | |||
| C4eEcPoint *C4E_RESTRICT | pt3 | |||
| ) |
Addition of two points on an elliptic curve 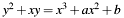 over the binary field
over the binary field  .
.
The algorithm calculates (according to IEEE Std 1363, annex A.10.2): ![$ P_3=P_1+P_2=(\lambda^2 \oplus \lambda \oplus x_1 \oplus x_2 \oplus a, \lambda[x_1 \oplus x_3] \oplus x_3 \oplus y_1) $](form_86.png) , with
, with 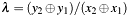 .
.
- Note:
- This function also works in case
pt1==pt2.
- Precondition:
pt3->x.digitsandpt3->y.digitsmust point to pre- allocated memory space for at leastdom->m.val.sizedigits.-
tmpmust point to pre-allocated memory space for at least (4U * C4E_GF2N_INV_SPACE(dom->m.val.size)) digits. - All domain parameters must be validated in advance.
-
All coordinate values must be reduced to modulus
dom->m.valand normalized, e.g. by using functions c4e_elem_norm() or c4e_elem_os2e().
- Bibliography:
- Standard Specifications For Public-Key Cryptography. Std 1363-2000, IEEE, 2000.
- Bibliography:
- Hankerson, Darrel, Alfred Menezes und Scott Vanstone: Guide to Elliptic Curve Cryptography. Springer, New York, 2004.
- Parameters:
-
[in] dom Pointer to domain parameters. [in] pt1 Pointer to first EC point. [in] pt2 Pointer to second EC point. tmp Array of temporary space elements (see preconditions for details on size). [out] pt3 Result of adding the EC points pt1andpt2, with all coordinate values normalized. The memberpt->attrmay indicate an error.
- Returns:
- Status
- Return values:
-
C4E_STATUS_OK if the calculation was successful other if the calculation has failed
| C4eSysStatus c4e_ecgf2n_dbl | ( | C4E_CONST C4eEcDomain *C4E_RESTRICT | dom, | |
| C4E_CONST C4eEcPoint *C4E_RESTRICT | pt, | |||
| C4eArchDigit | tmp[C4E_RESTRICT], | |||
| C4eEcPoint *C4E_RESTRICT | pt3 | |||
| ) |
Point doubling on an elliptic curve 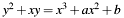 over the binary field
over the binary field  .
.
The algorithm calculates (according to IEEE Std 1363, annex A.10.2): ![$ P_3=2P=(\lambda^2 \oplus \lambda \oplus a, x^2 \oplus x_3[\lambda+1]) $](form_88.png) , with
, with 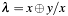 .
.
- Precondition:
pt3->x.digitsandpt3->y.digitsmust point to pre- allocated memory space for at leastdom->m.val.sizedigits.-
tmpmust point to pre-allocated memory space for at least (4U * C4E_GF2N_INV_SPACE(dom->m.val.size)) digits. - All domain parameters must be validated in advance.
-
All coordinate values must be reduced to modulus
dom->m.valand normalized, e.g. by using functions c4e_elem_norm() or c4e_elem_os2e().
- Bibliography:
- Standard Specifications For Public-Key Cryptography. Std 1363-2000, IEEE, 2000.
- Bibliography:
- Hankerson, Darrel, Alfred Menezes und Scott Vanstone: Guide to Elliptic Curve Cryptography. Springer, New York, 2004.
- Parameters:
-
[in] dom Pointer to domain parameters. [in] pt Pointer to EC point. tmp Array of temporary space elements (see preconditions for details on size). [out] pt3 Result of doubling the EC point, with all coordinate values normalized. The member pt3->attrmay indicate an error.
- Returns:
- Status
- Return values:
-
C4E_STATUS_OK if the calculation was successful other if the calculation has failed
- See also:
- c4e_elem_norm(), c4e_elem_os2e(), C4eEcPoint, C4E_ELEM_ASGN_MEM()
| C4eSysStatus c4e_ecgf2n_mul | ( | C4E_CONST C4eEcDomain *C4E_RESTRICT | dom, | |
| C4E_CONST C4eElement *C4E_RESTRICT | k, | |||
| C4E_CONST C4eEcPoint *C4E_RESTRICT | pt, | |||
| C4eArchDigit | tmp[C4E_RESTRICT], | |||
| C4eEcPoint *C4E_RESTRICT | kp | |||
| ) |
Point multiplication kP on an elliptic curve 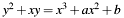 over the binary field
over the binary field  .
.
The calculation is performed by repeated multiply-add operations on a EC point. This is based on the binary representation of scalar k:
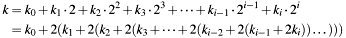
Multiplying this representation with curve point 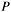 results in:
results in:
![\[ kP = k_0 P + 2 (k_1 P + 2 (k_2 P + 2 (k_3 P + \dots + 2 (k_{i-2} P + 2 (k_{i-1} P + 2 (k_i P))) \dots ))) \]](form_91.png)
- Note:
- This implementation uses affine coordinates in conjunction with the left-to-right binary algorithm. It does not make use of any algorithm associated with special curves (e.g. Koblitz curves) or any special modulus (e.g. trinomials).
- Precondition:
kp->x.digitsandkp->y.digitsmust point to pre- allocated memory space for at leastdom->m.val.sizedigits.-
tmpmust point to pre-allocated memory space for at least (6U * C4E_GF2N_INV_SPACE(dom->m.val.size)) digits. - All domain parameters must be validated in advance.
-
All coordinate values must be reduced to modulus
dom->m.valand normalized, e.g. by using functions c4e_elem_norm() or c4e_elem_os2e().
- Bibliography:
- Standard Specifications For Public-Key Cryptography. Std 1363-2000, IEEE, 2000.
- Bibliography:
- Hankerson, Darrel, Alfred Menezes und Scott Vanstone: Guide to Elliptic Curve Cryptography. Springer, New York, 2004.
- Parameters:
-
[in] dom Pointer to domain parameters. [in] k Number of point additions (big number). [in] pt Pointer to EC point. tmp Array of temporary space elements (see preconditions for details on size). [out] kp Result of EC point multiplication, with all coordinate values normalized. The member kp->attrmay indicate an error.
- Returns:
- Status
- Return values:
-
C4E_STATUS_OK if the calculation was successful other if the calculation has failed
| C4eSysBool c4e_ecgf2n_sign | ( | C4E_CONST C4eEcDomain *C4E_RESTRICT | dom, | |
| C4E_CONST C4eEcPoint *C4E_RESTRICT | pt, | |||
| C4eArchDigit | tmp[C4E_RESTRICT] | |||
| ) |
Returns the "sign" of coordinate 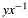 for an elliptic curve point over binary field
for an elliptic curve point over binary field  , according to IEEE Std 1363, annex A.9.6.
, according to IEEE Std 1363, annex A.9.6.
- Note:
- Does not realize the EC to octet string conversion primitive (EC2OSP) according to IEEE Std 1363, annex E.2.3.
- Precondition:
tmpmust point to pre-allocated memory space for at least (4U * C4E_GF2N_INV_SPACE(dom->m.val.size)) digits.- All domain parameters must be validated in advance.
-
All coordinate values must be reduced to modulus
dom->m.valand normalized, e.g. by using functions c4e_elem_norm() or c4e_elem_os2e(). - The function does not handle the pseudo-point at infinity. Use for example C4E_EC_IS_ZERO() to detect this situation in advance.
- Bibliography:
- Standard Specifications For Public-Key Cryptography. Std 1363-2000, IEEE, 2000.
- Parameters:
-
[in] dom Pointer to domain parameters. [in] pt Pointer to EC point. tmp Array of temporary space elements (see preconditions for details on size).
- Returns:
- Rightmost bit of the field element
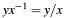 , expressed as
, expressed as C4E_TRUE(bit = 1) orC4E_FALSE(bit = 0). Ifpt->xis zero then it returnC4E_FALSE.
| C4eSysStatus c4e_ecgf2n_gety | ( | C4E_CONST C4eEcDomain *C4E_RESTRICT | dom, | |
| C4eSysBool | sign, | |||
| C4eArchDigit | tmp[C4E_RESTRICT], | |||
| C4eEcPoint *C4E_RESTRICT | pt | |||
| ) |
Calculates the y-coordinate associated with a x-coordinate for an elliptic curve over binary field  , according to IEEE Std 1363, annex A.12.9 and X9.62, section 4.2.2.
, according to IEEE Std 1363, annex A.12.9 and X9.62, section 4.2.2.
- Precondition:
tmpmust point to pre-allocated memory space for at least (5U * C4E_GF2N_INV_SPACE(dom->m.val.size)) digits.- All domain parameters must be validated in advance.
-
The coordinate value
pt->xmust be reduced to modulusdom->m.valand normalized, e.g. by using functions c4e_elem_norm() or c4e_elem_os2e().
- Bibliography:
- Standard Specifications For Public-Key Cryptography. Std 1363-2000, IEEE, 2000.
- Bibliography:
- Public Key Cryptography For The Financial Services Industry: The Elliptic Curve Digital Signature Algorithm (ECDSA). ANSI X9.62, 1998.
- Parameters:
-
[in] dom Pointer to domain parameters. [in] sign Sign of the y-coordinate (because there may be two), as defined by IEEE Std 1363, annex A.9.6. If pt->xis zero thensignis ignored.tmp Array of temporary space elements (see preconditions for details on size). [in,out] pt Pointer to EC point, with pt->xthe input andpt->youtput.
- Returns:
- Error status of calculation.
- Return values:
-
C4E_STATUS_OK if y-coordinate is valid (no error) C4E_STATUS_ERNG random generator failure C4E_STATUS_EDOM no solution in 
- See also:
- c4e_ecgf2n_sign()
| C4eSysStatus c4e_ecgf2n_validate | ( | C4E_CONST C4eEcDomain *C4E_RESTRICT | dom, | |
| C4E_CONST C4eEcPoint *C4E_RESTRICT | pt, | |||
| C4eArchDigit | tmp[C4E_RESTRICT] | |||
| ) |
Validates the coordinate values of an elliptic curve point are in range (fast) and optional verifies the point really is located on the elliptic curve over  .
.
In the first step (very fast) this function verifies if the coordinate values of point pt are elements of ground field  and so are in range.
and so are in range.
In a second step (optional, enabled when tmp is unequal to NULL) it validates the point pt as field of element of elliptic curve E, as specified in dom. In this case it verifies equation 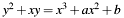 for elliptic curve point
for elliptic curve point pt.
- Note:
- Because the elliptic curve
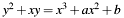 degenerates to
degenerates to 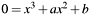 for
for 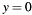 or to
or to 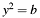 for
for 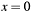 only one coordinate component (
only one coordinate component (pt->xorpt->y) is allowed to be zero.
- Precondition:
- If
tmpis unequal toNULL(extended test) then it must point to pre-allocated memory space for at least (2U * C4E_GF2N_INV_SPACE(dom->m.val.size)) digits. - All domain parameters must be validated in advance.
-
The coordinate values of
ptmust be normalized, e.g. by using functions c4e_elem_norm() or c4e_elem_os2e(). - The function does not handle the point zero at infinity. Use C4E_EC_IS_ZERO() to detect this situation in advance.
- Bibliography:
- Standard Specifications For Public-Key Cryptography. Std 1363-2000, IEEE, 2000.
- Bibliography:
- Public Key Cryptography For The Financial Services Industry: The Elliptic Curve Digital Signature Algorithm (ECDSA). ANSI X9.62, 1998.
- Bibliography:
- Hankerson, Darrel, Alfred Menezes und Scott Vanstone: Guide to Elliptic Curve Cryptography. Springer, New York, 2004.
- Parameters:
-
[in] dom Pointer to domain parameters. [in] pt Pointer to EC point to validate. tmp Array of temporary space elements (see preconditions for details on size). If tmpisNULLthen only a basic (but very fast) test of coordinate valuespt->xandpt->yis performed.
- Returns:
- C4E_STATUS_OK if the test was successful, else an error status.
- See also:
- C4E_EC_IS_ZERO(), c4e_elem_norm(), c4e_elem_os2e(), C4eEcPoint
 1.6.1
1.6.1