Elliptic Curve Digital Signature Algorithm (ECDSA)
[ECC over binary field]
Elliptic Curve Digital Signature Algorithm (ECDSA). More...
Functions | |
| C4eSysStatus | c4e_ecc2n_dsa_sign (C4eEcDomain *C4E_RESTRICT dom, C4E_CONST C4eElement *C4E_RESTRICT d, C4eHashId hid, C4E_CONST C4eArchUint8 *C4E_RESTRICT digest, C4eArchDigit tmp[C4E_RESTRICT], C4eArchUint8 *C4E_RESTRICT signature) |
ECDSA over  signature of a digest, according to ANSI X9.62 and FIPS 186-4, with binary encoded signature. signature of a digest, according to ANSI X9.62 and FIPS 186-4, with binary encoded signature. | |
| C4eSysStatus | c4e_ecc2n_dsa_verify (C4eEcDomain *C4E_RESTRICT dom, C4E_CONST C4eEcPoint *C4E_RESTRICT q, C4eHashId hid, C4E_CONST C4eArchUint8 *C4E_RESTRICT digest, C4E_CONST C4eArchUint8 *C4E_RESTRICT signature, C4eArchSize len, C4eArchDigit tmp[C4E_RESTRICT]) |
ECDSA over  signature verification, according to ANSI X9.62 and FIPS 186-4, with binary encoded signature. signature verification, according to ANSI X9.62 and FIPS 186-4, with binary encoded signature. | |
Detailed Description
Elliptic Curve Digital Signature Algorithm (ECDSA).
Function Documentation
| C4eSysStatus c4e_ecc2n_dsa_sign | ( | C4eEcDomain *C4E_RESTRICT | dom, | |
| C4E_CONST C4eElement *C4E_RESTRICT | d, | |||
| C4eHashId | hid, | |||
| C4E_CONST C4eArchUint8 *C4E_RESTRICT | digest, | |||
| C4eArchDigit | tmp[C4E_RESTRICT], | |||
| C4eArchUint8 *C4E_RESTRICT | signature | |||
| ) |
ECDSA over  signature of a digest, according to ANSI X9.62 and FIPS 186-4, with binary encoded signature.
signature of a digest, according to ANSI X9.62 and FIPS 186-4, with binary encoded signature.
The Elliptic Curve Digital Signature Algorithm (ECDSA) is based on the following formulas for calculating the signature (r,s):
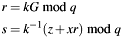
with z the (partial) digest, G the base point, k the (random) one-time private key, d the private key and q the order of base point G in binary field  .
.
- Note:
- The first signature part r is also called one-time public key.
-
Because of the randomness of the one-time private key k each signature differs from another, also if private key
danddigestare the same as in the previous one.
- Attention:
- The domain parameter
dom->qis temporary modified - so it must be writable. After function return it holds the same values as at function entry.
- Precondition:
- The validity of the EC domain parameters in
dommust be assured by the caller, either implicit or by using function c4e_ecc2n_domchk(). -
The validity of the private key
dmust be assured by the caller, either implicit or by using function c4e_ecc2n_keychk_prv(). -
The caller must provide the following digits space in array
tmp[]:- for nearly all well-known elliptic curves (satisfying
dom->q.val.size<=dom->m.val.size), by using macro C4E_ECC2N_TMP_NUM() in conjunction with temp. space qualifier C4E_ECC2N_DSA_TMPID_SIGN; - for special (very uncommon/rare) elliptic curves with
dom->q.val.size>dom->m.val.sizeusing the exact value:or worst-case:8U * C4E_GF2N_INV_SPACE(dom->m.val.size) + C4E_GFP_INV_SPACE(dom->q.val.size)
Recommendation: Simply use C4E_ECC2N_DSA_TMPID_SIGN, but test (as sanity check) the elliptic curve for:8U * C4E_GF2N_INV_SPACE(dom->m.val.size) + C4E_GFP_INV_SPACE(C4E_EC_FIELD_DIGITS_MAX(dom->m.val.size))
dom->q.val.size <= dom->m.val.size
- for nearly all well-known elliptic curves (satisfying
- The Random Number Generator (RNG) must be initialized at user side, then installed via function c4e_rng_install().
- Bibliography:
- Digitale Signature Standard (DSS). FIPS Publication 186-4, National Institute of Standards and Technology, 2013.
- Bibliography:
- Public Key Cryptography For The Financial Services Industry: The Elliptic Curve Digital Signature Algorithm (ECDSA). ANSI X9.62, 1998.
- Bibliography:
- Standard Specifications For Public-Key Cryptography. Std 1363-2000, IEEE, 2000.
- Parameters:
-
[in] dom Pointer to EC domain parameters. [in] d Pointer to private key d<dom->q.[in] hid Hash algorithm identifier associated with digestand it's length.[in] digest Digest calculated by the caller using a hash function. tmp Array of temporary space elements (see preconditions for details on size). [out] signature Signature buffer, with implicit length of (2U * dom->q.len) bytes. It is binary encoded according to IEEE Std 1363, annex E.3.1.
- Returns:
- Status
- Return values:
-
C4E_STATUS_OK If the operation was successful. other If the operation has failed.
| C4eSysStatus c4e_ecc2n_dsa_verify | ( | C4eEcDomain *C4E_RESTRICT | dom, | |
| C4E_CONST C4eEcPoint *C4E_RESTRICT | q, | |||
| C4eHashId | hid, | |||
| C4E_CONST C4eArchUint8 *C4E_RESTRICT | digest, | |||
| C4E_CONST C4eArchUint8 *C4E_RESTRICT | signature, | |||
| C4eArchSize | len, | |||
| C4eArchDigit | tmp[C4E_RESTRICT] | |||
| ) |
ECDSA over  signature verification, according to ANSI X9.62 and FIPS 186-4, with binary encoded signature.
signature verification, according to ANSI X9.62 and FIPS 186-4, with binary encoded signature.
The Elliptic Curve Digital Signature Algorithm (ECDSA) is based on the following formulas for verification of the signature (r,s):
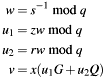
with z the (partial) digest, G the generator, Q the public key and q the order of base point G in binary field  . The condition for a correct signature is:
. The condition for a correct signature is: 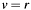 .
.
- Attention:
- The domain parameter
dom->qis temporary modified - so it must be writable. After function return it holds the same values as at function entry.
- Precondition:
- The validity of the EC domain parameters in
dommust be assured by the caller, either implicit or by using function c4e_ecc2n_domchk(). -
The validity of ECDSA public key
qmust be assured by the caller, for example by using function c4e_ecc2n_keychk_pub(). -
The caller must provide the following digits space in array
tmp[]:- for nearly all well-known elliptic curves (satisfying
dom->q.val.size<=dom->m.val.size), by using macro C4E_ECC2N_TMP_NUM() in conjunction with temp. space qualifier C4E_ECC2N_DSA_TMPID_VERIFY; - for special (very uncommon/rare) elliptic curves with
dom->q.val.size>dom->m.val.sizeusing the exact value:or worst-case:12U * C4E_GF2N_INV_SPACE(dom->m.val.size) + 2U * C4E_GFP_INV_SPACE(dom->q.val.size)
Recommendation: Simply use C4E_ECC2N_DSA_TMPID_VERIFY, but test (as sanity check) the elliptic curve for:12U * C4E_GF2N_INV_SPACE(dom->m.val.size) + 2U * C4E_GFP_INV_SPACE(C4E_EC_FIELD_DIGITS_MAX(dom->m.val.size))
dom->q.val.size <= dom->m.val.size
- for nearly all well-known elliptic curves (satisfying
- Bibliography:
- Digitale Signature Standard (DSS). FIPS Publication 186-4, National Institute of Standards and Technology, 2013.
- Bibliography:
- Public Key Cryptography For The Financial Services Industry: The Elliptic Curve Digital Signature Algorithm (ECDSA). ANSI X9.62, 1998.
- Bibliography:
- Standard Specifications For Public-Key Cryptography. Std 1363-2000, IEEE, 2000.
- Parameters:
-
[in] dom Pointer to EC domain parameters. [in] q Pointer to ECDSA public key, a curve point. [in] hid Hash algorithm identifier associated with digestand it's length.[in] digest Digest calculated by the caller using a hash function. [in] signature Signature to be verified. It must be binary encoded according to IEEE Std 1363, annex E.3.1. [in] len Length of signaturein bytes.tmp Array of temporary space elements (see preconditions for details on size).
- Returns:
- Status
- Return values:
-
C4E_STATUS_OK If the signature is valid. other If the signature verification has failed.
 1.6.1
1.6.1